The Normal Distribution and the 68-95-99.7 Rule
In this article, we’ll be learning about The Normal Distribution and the 68-95-99.7 Rule when we talk about normal distributions we refer to data we get from a population or sample.
The difference between a Parameter and a Statistic
A parameter is a number that describes the data from a population whereas a statistic is a number that describes the data from a sample Examples of parameters and statistics are the mean and standard deviation but because of the definitions we just talked about we have to be very careful with what symbols we use to represent these numbers when we are dealing with a sample we use the symbol x-bar to represent the sample mean and we use the letter s to represent the sample standard deviation these are statistics when we are dealing with a population we use the Greek letter μ to represent the population Mean and we use the Greek letter σ to represent the population standard deviation these are parameters the population parameters μ and σ are very important when we talk about normally distributed populations.
What is a normal distribution?
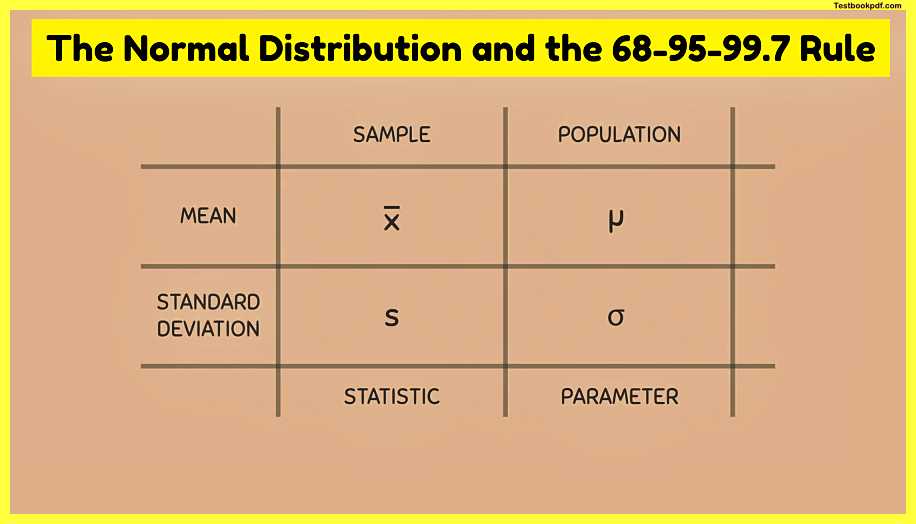
A normal distribution is a special type of density curve that is bell-shaped for this reason the normal distribution is sometimes called the bell curve or the normal curve the normal distribution describes the tendency for data to cluster around a central value in fact this central value is the population mean μ which is always located in the middle of the curve so for any normal distribution we can say that some data points will fall below the mean other data points will fall above the mean but most of the data values are located near the mean the normal distribution and its shape actually arises from many different variables found in nature such as weight height volume blood pressure and many more this is why the normal distribution is commonly studied for example exam scores are known to follow a normal distribution some people do great on exams some people do poorly on exams but a large majority of people score near the average or the mean in this example the average exam score is 50 because it is located in the middle of the curve now that you know what a normal distribution looks like we need to talk about the population mean meal and the population standard deviation σ both of these tell us important information about how the normal distribution looks.
Effects of the Mean μ on the Normal Curve
We all talk about the population mean μ first, the population mean μ characterizes the position of the normal distribution if you increase the mean the curve will follow and move towards the right, and if you decrease the mean the curve will still follow and move towards the left this happens because the data will always cluster around the mean in normally distributed populations, as a result, the value of the mean determines the position of the normal distribution.
Effects of the Standard Deviation Sigma (σ) on the Normal Curve
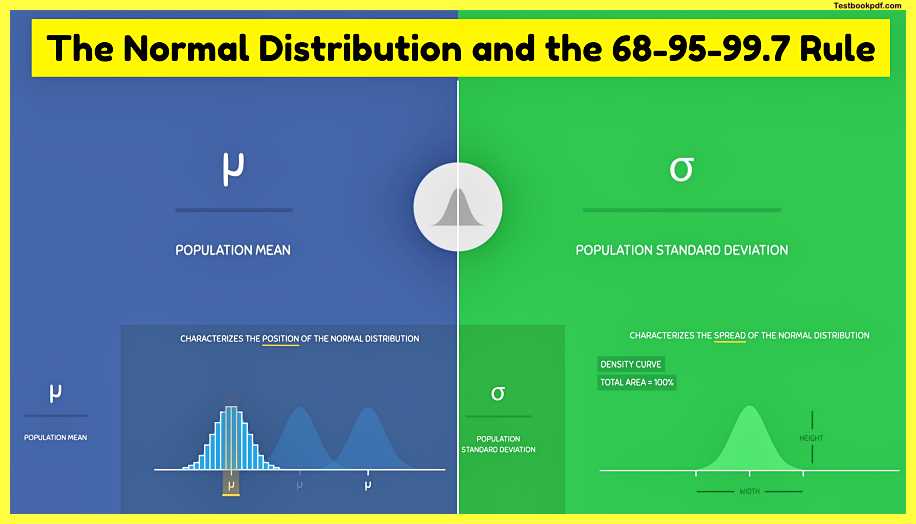
On the other hand, the population standard deviation σ characterizes the spread of the normal distribution the larger the standard deviation the more spread out the distribution will be and the smaller the standard deviation the less spread order will be noticed that when the spread increases the curve gets much flatter and when the spread decreases the curve gets taller the reason for this is because the normal distribution is a density curve and the total area of any density curve must remain equal to one or a 100% so changes in the width of the curve must be compensated for by changes in the height of the curve and vice versa.
Characteristic Overview of the Normal Distribution

Overall here are some points about the normal distribution, the normal distribution is unimodal which means that the distribution has a single peak the normal curve is symmetric about its mean so you can clearly see that the distribution can be cut into two equal halves the parameters μ and σ completely characterized the normal distribution the population means μ determines the location of the distribution and where the data tends to cluster around the population standard deviation σ determines how to spread out the distribution will be the notation given to a population that follows a normal distribution can be written like this although it looks scary it means what it says for the variable X it follows a normal distribution and has the mean μ with a standard deviation of σ now that you’ve been introduced to the normal distribution.
The 68-95-99.7 Rule
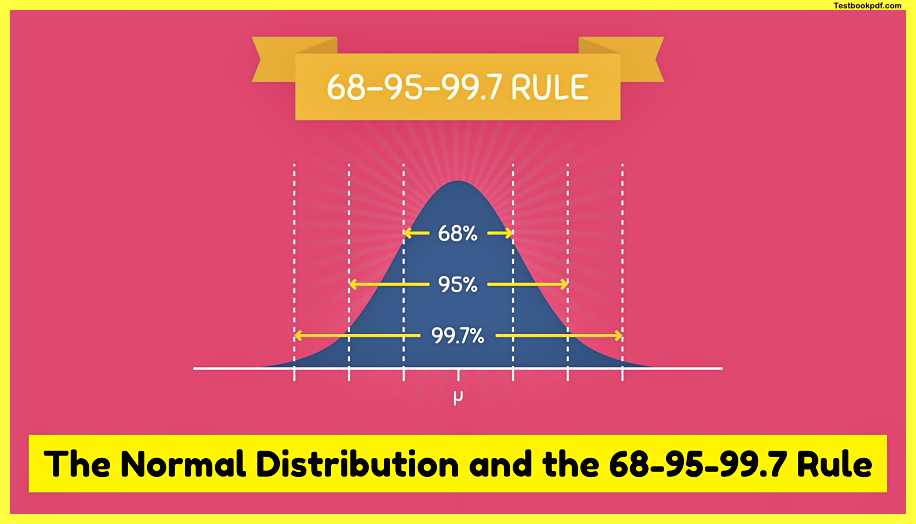
If we were measuring the heights of all students at a local university and found that it was normally distributed with a mean height of 5.5 feet and a standard deviation of half a foot or 0.5 we can construct a normal distribution as follows from here we can create intervals that increase by the standard deviation so we’ll have 66.5 and 7 and on the other side, we’ll have 54.5 and four so what the 68 95 99 point seven rule says is that within one standard deviation away from the mean it contains a total area of zero point six eight or 68% because of this we can say that 68% of the population are between five and six feet tall and if he goes to standard deviations away from the mean it contains an area of 95% this means that 95% of the people in the population have a height between four point five and six point five feet and finally within three standard deviations away from the mean it contains a total area of 99.7% this means that for the population we are studying 99.7% of the people are between four and seven feet tall now you might be wondering what happens if we go four standard deviations away from the mean or five or six standard deviations away from the mean and to answer that you actually can a normal distribution actually never touches the x-axis it continues on to infinity so you can go as many standard deviations away from the mean as you want but the area contained within these regions will be very very small the 6895 99.7 rule is a great way for approximating the areas of a normal distribution and this works for any normal distribution no matter what shape and size.
Practice Question #1
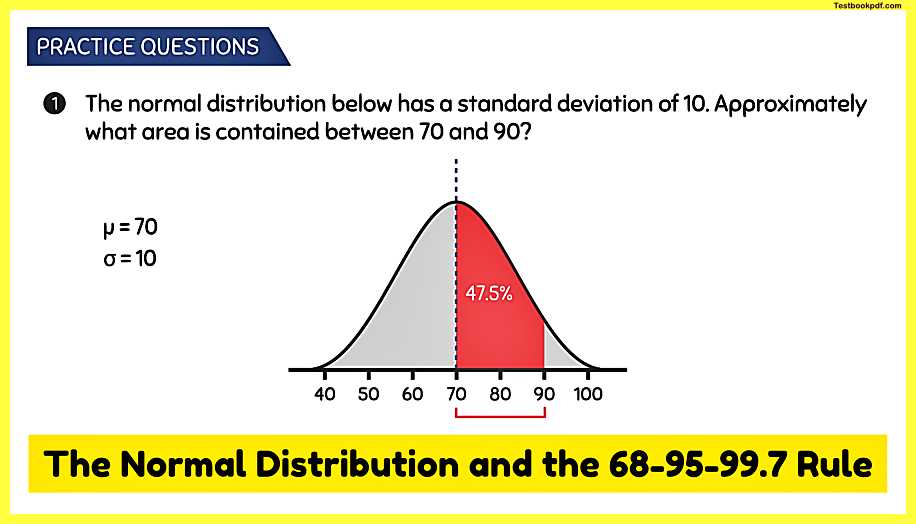
Q1: The normal distribution below has a standard deviation of 10 approximately what area is contained between 70 and 90?
A: in this question, we know that the population Mean is equal to 70 because it’s in the center of the distribution we also know from the question that one standard deviation is equal to 10 and we can see this because each interval goes up by 10 according to the 6895 99.7 rule we know that there is an area of 95% contained within two standard deviations of the mean two standard deviations to the right gets us to 90 and two standard deviations to the left get us to 50 according to the 68-95-99.7 rule this means that there is an area of 95% contained within this interval however we are only interested in the area from 70 to 90 so dividing this area by two gives us our area of interest 95% divided by two gives us an area of 47.5% and that is our answer.
Practice Question #2
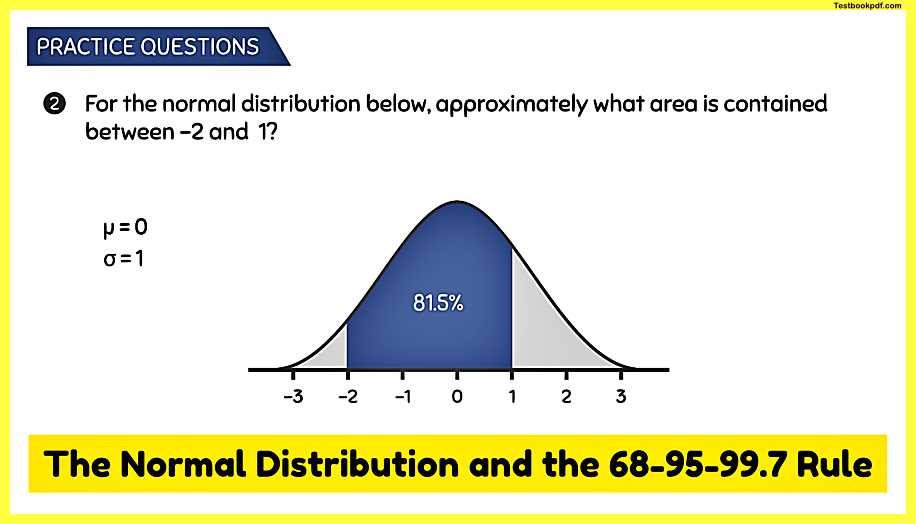
Q2: what area is contained between negative two and one?
A: In this example, we know that we have am u of zero because zero is in the center of the distribution and we know that we have a σ of one because each interval goes up by one to approximate the area between negative two and one we use the 6895 99.7 rule we can strategically divide this area into two parts so that we can easily incorporate this rule we’ll start with the right half which goes from zero to one we know that one standard deviation away from the mean gives us 68% and half of this is 34% giving us our area from zero to one the next half goes from zero to negative two but we know that within two standard deviations from the mean we have an area of 95% dividing this by two gives us the area from zero to negative two which is equal to 47.5% and finally to get that total area contained between negative two and one all we have to do is add these two areas together and when we do we get a total area of 81.5%


